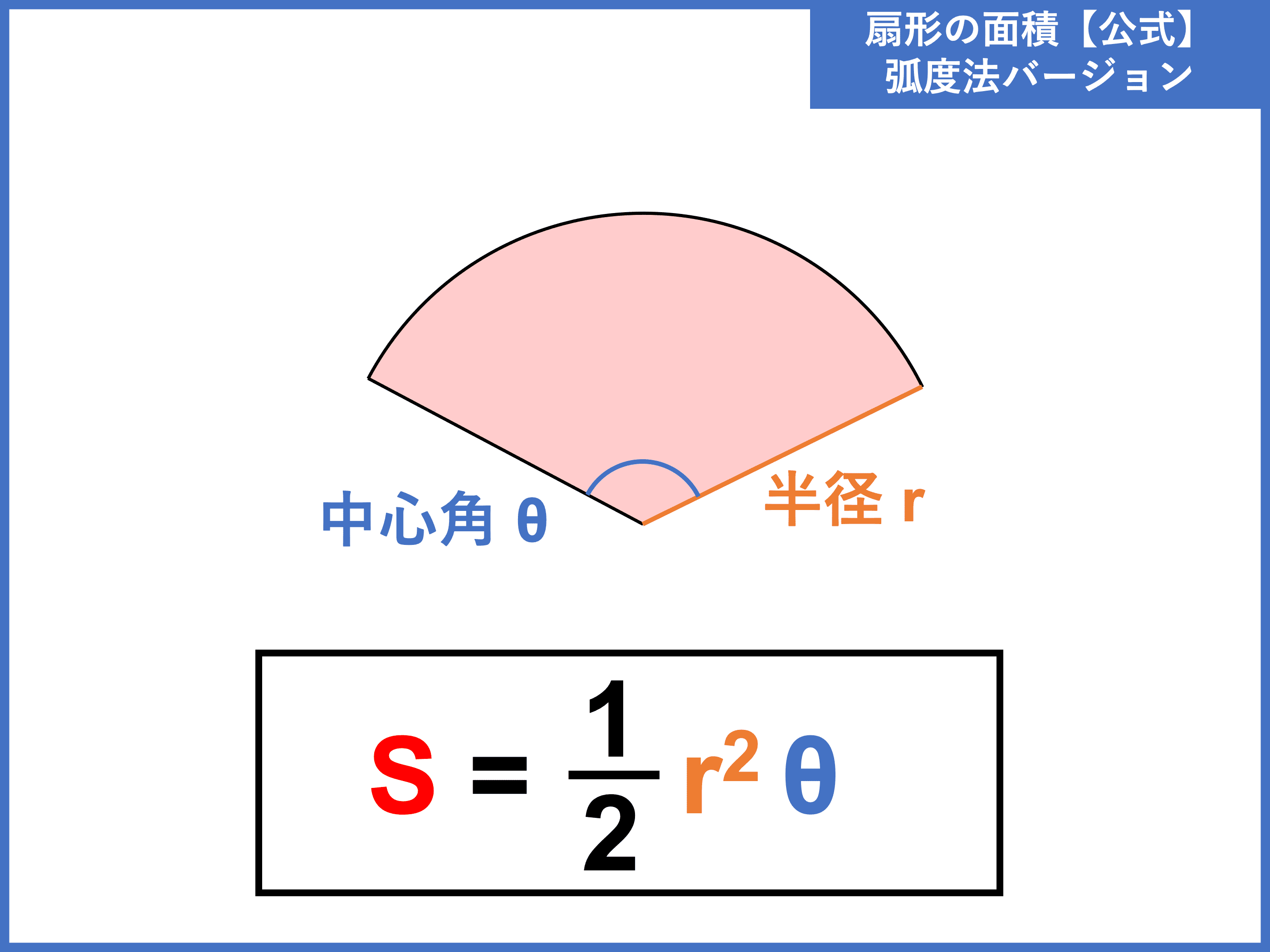
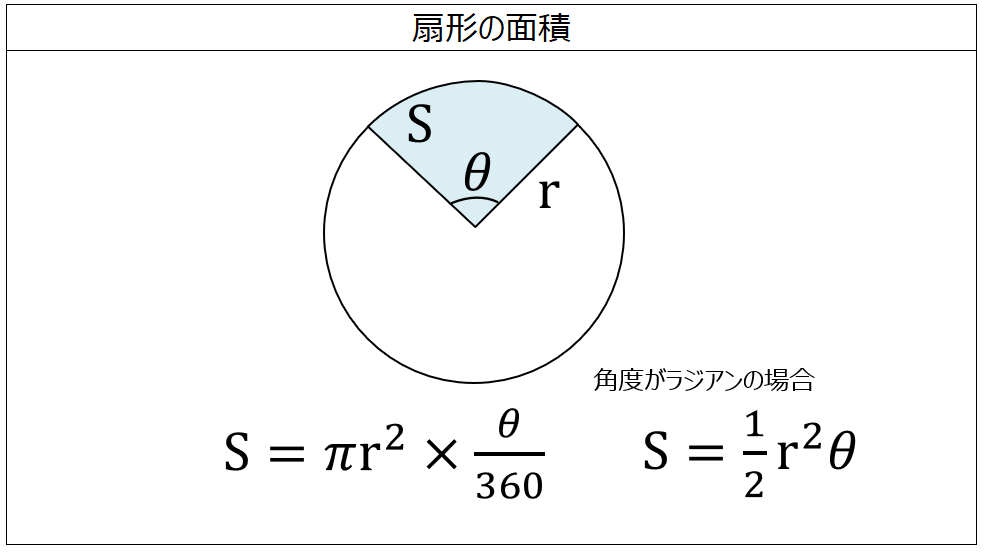
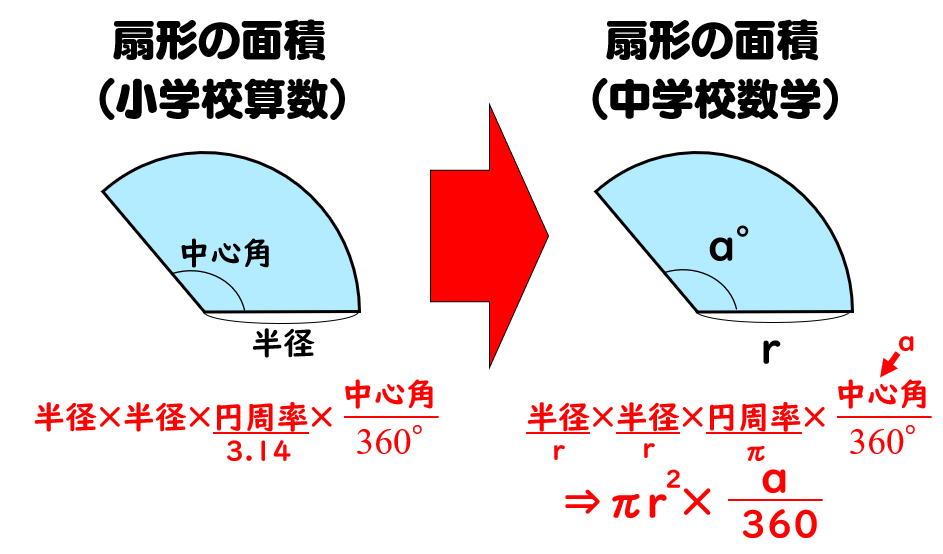
現代の数学教育において、円や扇形の面積計算は重要なテーマとして取り上げられています。このテーマは、単なる数式の暗記だけでなく、幾何学的思考を育てるための基礎的なスキルを涵養するものです。例えば、円の面積を求める公式は、面積 = 半径 × 半径 × 3.14 で表されますが、この公式の背後には多くの応用可能性が隠されています。また、扇形の面積を求める場合、その公式はさらに複雑になり、面積 = 半径 × 半径 × 3.14 × 中心角 ÷ 360° となります。
これらの公式は、数学の基本的な要素である円周率 π(3.14)を用いて計算されます。円周率 π は、古来より多くの数学者を魅了し続けてきた数値で、その無限に続く小数点以下の桁数は、数学の深遠さを象徴しています。近年では、円周率 π を用いた計算は、単なる数学の範囲にとどまらず、工学、物理学、さらにはコンピュータサイエンスの分野でも活用されています。例えば、NASAの探査機の軌道計算や、人工衛星の設計においても、円周率 π の精度が求められています。
| 項目 | 詳細 |
|---|---|
| 氏名 | 円周率 π |
| 生年月日 | 古代から存在(具体的な発見年は不明) |
| 出身地 | 古代文明(バビロニア、エジプトなど) |
| 職業 | 数学的定数 |
| 主な業績 | 円周の長さと直径の比率を示す |
| 関連リンク | 円周率に関する公式サイト |
円周率 π の歴史を紐解くと、これは単なる数値を超えて、多くの著名な数学者たちを引き寄せました。例えば、古代ギリシャの数学者アーキメデスは、円周率 π をより正確に計算するために、多角形の内接と外接を用いた方法を考案しました。また、近代に至り、ライプニッツやオイラーなどの数学者たちも、円周率 π の研究に多大な貢献をしました。
Read also:Amazon Stock The Ultimate Guide For Investors In 2023
現代において、円や扇形の面積計算は、日常生活でも頻繁に応用されています。例えば、建築設計においては、円形の建物や庭園の面積を計算する必要があります。また、自動車のタイヤや飛行機のプロペラの設計にも、円周率 π が活用されています。さらに、音響エンジニアリングの分野では、音波の円形パターンを解析するために円周率 π を使用しています。
これらの応用は、現代社会に大きな影響を与えています。例えば、スマートフォンのカメラセンサーにおいても、円形の光学レンズの設計が不可欠であり、その設計には円周率 π が不可欠です。また、医療分野では、MRIやCTスキャンの画像解析にも円周率 π が活用されています。このように、円周率 π は、数学という枠を超えて、私たちの日常生活に深く関わっています。
さらに、円や扇形の面積計算は、芸術の世界でも重要な役割を果たしています。例えば、建築家の扎哈・ハディドが手掛けた多くの建築物は、曲線や円形を大胆に取り入れており、その設計には円周率 π の正確な計算が欠かせません。また、現代アートにおいても、円や扇形をモチーフにした作品が数多く存在します。これらの作品は、数学的な正確さと芸術的な感性を融合させたものであり、観る人々に深い印象を与えています。
一方で、円や扇形の面積計算は、教育現場でも重要な役割を果たしています。特に、中学生や高校生向けの数学教育では、これらの公式を用いた問題が頻繁に出題されます。この教育の目的は、単なる公式の暗記ではなく、数学的思考力を養うことにあります。例えば、扇形の面積を求める際に、中心角の比率を考慮する必要があるため、生徒たちは比例の概念を理解する必要があります。また、半径や円周率 π の関係性を理解することで、数学的な応用力を高めることができます。
円や扇形の面積計算は、さらに広がる応用可能性を持っています。例えば、人工知能(AI)の分野でも、円周率 π を用いた計算が行われています。AIが画像認識を行う際に、円形の物体を正確に認識するためには、円周率 π を用いた幾何学的な解析が必要です。また、自動運転車の開発においても、車両周辺の円形エリアを監視するために、円周率 π の計算が活用されています。
さらに、スポーツの分野でも円や扇形の面積計算は応用されています。例えば、サッカーのゴールエリアやバスケットボールの3ポイントラインは、円形や扇形を基に設計されており、その面積の計算には円周率 π が不可欠です。また、陸上競技の円盤投げやハンマー投げにおいても、円形の投擲エリアの面積を正確に計算する必要があります。
Read also:Trump News The Inside Scoop On Politics Drama And Everything Inbetween
これらの応用例は、円や扇形の面積計算がいかに多岐にわたる分野で活用されているかを示しています。また、円周率 π 自体が持つ神秘的な性質は、多くの人々を引き寄せ、研究を進展させる原動力となっています。例えば、円周率 π の小数点以下の桁数を競うコンテストが毎年開催され、記録を更新する人々がいます。このような活動は、数学への関心を高めるきっかけとなっています。
最後に、円や扇形の面積計算は、社会全体に与える影響も大きく、その重要性は今後も増していくでしょう。特に、AIや自動運転技術の進展に伴い、円周率 π を用いた計算の需要はさらに高まることが予想されます。そのため、数学教育においても、円や扇形の面積計算をより実践的な視点から学ぶことが求められています。